For centuries, we have known that the world around us can be explained by the scientific method. The difficulty was always making the discoveries within science to do so. However, the existence of mathematics has made it a lot easier for us. We can see mathematics in nature – numerical patterns within sunflowers and breeding ratios – formulas have been used to predict the discoveries of mathematical anomalies like black holes. Some say our universe is literally made out of mathematics in the same way that computer programmes are made out of code. Everything we can observe has a mathematical explanation, even the most complex and beautiful of anomalies. This is a list of 10 epic examples of mathematics in nature.

Black Holes

The existence of black holes was originally discovered by a mathematician. But they had no idea what it was – just that the formula behind black holes was a true mathematical anomaly. For this reason, black holes easily belong on our list of examples of mathematics in nature. Only quantum theory would give us a more deep understanding of black holes. Stephen Hawking was able to learn that they do emit radiation in the 1970s. Despite the original theory that literally nothing can escape black holes, it is now thought that some information can escape. And since 2014, it is thought that a tiny amount of light is able to escape also. It is thought that there is a black hole in the centre of every galaxy. For a black hole to be created, mass have to be compressed enough for it to collapse into itself. There is a mathematical formula for this – planet Earth would become a black hole if compressed to the size of a walnut. It truly is one of the more awe inspiring examples of mathematics in nature.

DNA

DNA is vital to all living organisms. It contains much of the genetic code that allows us to grow, function, and produce new life via reproduction. How we live changes our DNA and our DNA affects how we live and age. DNA damage is not a harmless thing, without it we couldn’t exist. The structure of DNA correlates to numbers in the Fibonacci sequence, with an extremely similar ratio. The Fibonacci sequence is a mathematical pattern that correlates to many examples of mathematics in nature. This includes rabbit breeding patterns, snail shells, hurricanes and many many more examples of mathematics in nature. It was named after the man who discovered it, Fibonacci, who some call the greatest European mathematician of the middle-ages. Clearly, DNA structure is related to the Fibonacci numbers.

Snowflakes

Snowflakes certainly are a beautiful glimpse of mathematics in nature. A snowflake is an ice crystal that falls from the sky. But what about the mathematics? Well, it’s all about the symmetry. Each arm of a snowflake is identical, unless it has been damaged. This seems quite simple at first but it has troubled science for quite a long time. Especially considering the fact that every snowflake is unique in terms of it’s structure. How could they all be unique – yet symmetrical? The answer is that their bonds need to be symmetrical or they won’t be strong enough to stay together – and that each snowflake falls from the sky under unique conditions, causing it to be differently shaped than any other.

Sunflower Heads

For sunflower heads we must return to the Fibonacci sequence. The Fibonacci sequence can be seen in so many flower seed spirals and petal growth. On a sunflower head, the seeds grow from the centre before continuing to grow outwards to fit the pattern. And when I say the pattern, I mean the standard spiral pattern for several type of plant seeds. The pattern just so happens to correlate to the Fibonacci sequence. I hope you’re not already sick of Fibonacci because it manifests itself in many examples of mathematics in nature (so expect more soon!).

Honeycombs

Everyone love honey, it tastes nice and honey is a nice sounding word. Even bears love it. It is one of the few edible substances that never goes bad. They have even found still edible honey inside ancient Egyptian tombs. Bees build honeycombs as a place to store the honey they create. The shape of honeycombs is an extremely good compromise between strength and space needed for storage. In fact, mathematicians go so far as to say that no other structure would be better for it’s purposes. And that is why honeycombs are an epic example of mathematics in nature.

The Eclipse

We always have at least one eclipse each year, and they’re quite fun. I remember watching a rather significant eclipse in the year 2000, there won’t be a longer eclipse until the year 3000! An eclipse in when the moon and the Earth align to the point where sunlight is completely blocked out. It’s an amazing sight, and an epic example of mathematics in nature. This is of course only possible due to the size of the moon relative to the size of the sun. The sun is 1.4 million kilometres, whereas the moon is about 3.5 thousand kilometres – a huge difference! But the sun is a lot further away from us than the moon is. This perspective allows them to align just right for the perfect eclipse. It’s by complete chance that the planets can align like this, and we have no idea whether it’s common for plants to be like ours in that respect… but we haven’t found much. According to science the moon is slowly moving further away from the Earth. If that continues, our eclipses may eventually cease to exist.

Shells
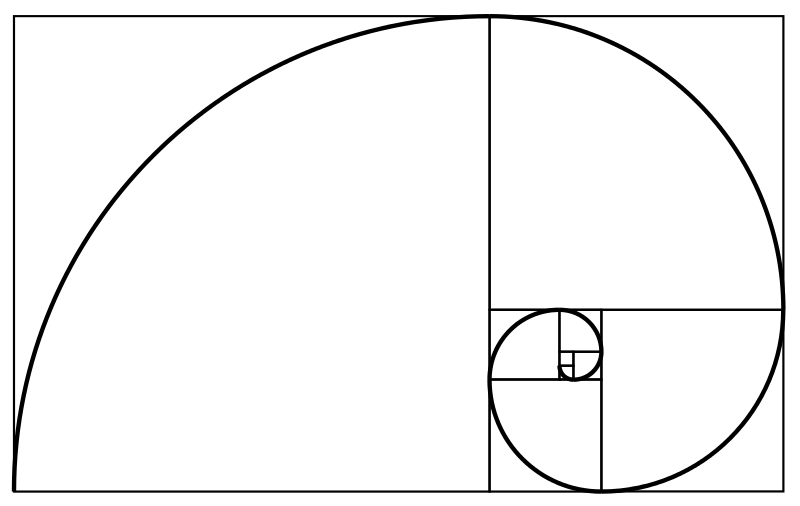
There is a mathematical structure called the golden ratio. It is based on the Fibonacci sequence and can be translated into the golden spiral. The golden spiral is directly proportional to the structure of certain shells. As you’ll see from the image above, just a standard diagram of the spiral looks exactly like a shell. The shape of a shell always stays the same, it just gets larger. It’s one of the more expected manifestations of mathematics in nature.

Spider Webs

There is a type of spider Web called an orb web. Orb spiders create webs that are nearly completely symmetrical – and also nearly completely circular. The spiders seem to have a natural ability to judge geometrical distance with astounding accuracy. We don’t know how they do it, but they do. We don’t even know why they do it. Maybe they do it for strength purposes. Or maybe they’re just dumb spiders who don’t know what they’re doing. Either way, it’s top rate mathematics in nature.

Human Features

Human facial features also fall to the mighty golden ratio. There are even studies that show humans who have facial features more accurately related to the golden ratio tend to be considered more physically attractive than those less mathematically holy. No one said that mathematics in nature would be equally kind to us.

Galaxies

Galaxies are kinda weird when you think about it. Spiral galaxies correlate to the now famous golden ratio. It’s pretty much the same mathematical pattern as a hurricane of snails shell. But mathematics in nature covers more than the Fibonacci numbers. Our own galaxy, the milky way, is incredibly mathematical. Apparently it is near-symmetrical, as if one half is a mirror image of the other.

